好(hǎo)吧，不知(zhī)道(dào)你(nǐ)們是不是看(kàn)上(shàng)瘾了(le)，反正小(xiǎo)編我是寫上(shàng)瘾了(le)，今天咱們接着來(lái)
1）引言
上(shàng)一篇我們介紹了(le)直流電機的基本結構，也(yě)順便回憶了(le)一下(xià)童年，這(zhè)一篇我們具體介紹電磁的轉換過程與直流電機的輸出功率、轉矩等
2）磁場
還是先上(shàng)圖
第一篇文(wén)章《【希騰通用(yòng)技術課堂】電機基礎》裏面我們有介紹到(dào)過公式2-磁通量，公式3-安培定律等，如果進行更加精細的分析，可能(néng)會(huì)遇到(dào)構形上(shàng)的問題和(hé)鐵(tiě)芯的磁飽和(hé)問題，爲了(le)更準确的分析，通常也(yě)會(huì)用(yòng)例如有限元分析的方式來(lái)進行建模分析。在一些(xiē)精度不是非常高(gāo)的場合，使用(yòng)簡化近似方程是一個十分行之有效的方法，當然我們也(yě)必須要用(yòng)到(dào)第一篇裏面的一些(xiē)基本假設：
· 鐵(tiě)芯磁導率
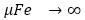，也(yě)就是說，電機的鋼鐵(tiě)部分的勵磁可以忽略不計(jì)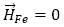 
· 氣隙
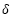（定子與轉子間的間隙）保持不變· 氣隙處的漏磁忽略不計(jì)
理(lǐ)想情況下(xià)，氣隙中是一個恒定磁感強度的純輻散場，并且極缺口處沒有漏磁。而實際情況是極靴的形狀、定子形狀本身也(yě)有一定的公差，氣隙的寬度也(yě)會(huì)産生一些(xiē)變化，因此磁場線并非是一個完美(měi)的長方形
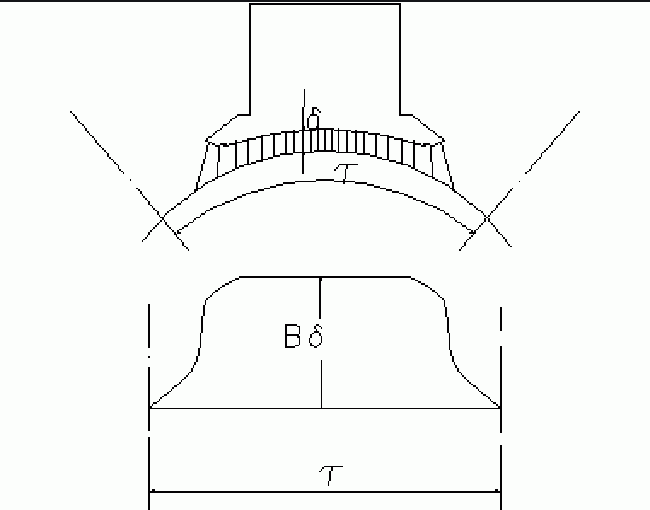
爲了(le)便于計(jì)算(suàn)，我們可以把原函數的均值乘以新的極寬，獲得一個等效方形函數，這(zhè)裏我們會(huì)用(yòng)到(dào)一個極覆蓋率的概念
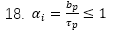
通常極覆蓋率的範圍大(dà)約在0.6到(dào)0.8之間，極覆蓋率越高(gāo)，那麽更多的磁場會(huì)從(cóng)極到(dào)極通過，越低(dī)，就會(huì)産生更多的漏磁
我們把磁通做一個積分就可以獲得最大(dà)磁通
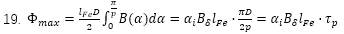
其中l是電機軸向的長度
3）轉矩
我們知(zhī)道(dào)，導體在勵磁磁場中旋轉時(shí)會(huì)産生感應電壓
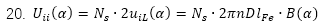
2a爲并聯支路數量，則可以計(jì)算(suàn)出串聯的支路裏面的線圈數是
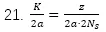
K爲換向片的片數，在不同繞組形式裏面2a也(yě)不同，結合上(shàng)面我們提到(dào)的極覆蓋率，整個支路的感應電壓爲
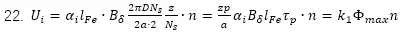
其中
，這(zhè)樣，我們就算(suàn)出來(lái)了(le)直流電機的感應電壓、磁通和(hé)轉速的關系
如果我們把電源本身的電壓也(yě)算(suàn)進去的話(huà)
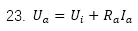
R和(hé)I是電樞上(shàng)的電阻和(hé)電壓，根據公式13，磁場裏面的每根導體都會(huì)受到(dào)的力爲
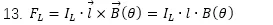
氣隙裏面有效導體數量爲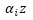
，所有的導體所受到(dào)的作(zuò)用(yòng)力和(hé)扭矩爲
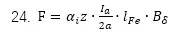
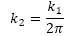
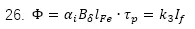
4）功率和(hé)損耗
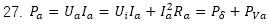
上(shàng)面這(zhè)個公式是直流電機電樞所需的功率，其中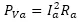
，是電阻的熱損耗功率，實際還會(huì)有電刷的損耗，即
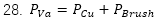
電刷的功率損耗主要是換向時(shí)候的壓降
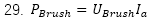
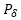爲氣隙功率，是從(cóng)定子傳導到(dào)轉子的功率
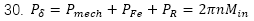
轉子在軸承上(shàng)和(hé)空(kōng)氣會(huì)有機械摩擦，帶來(lái)的損耗
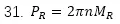
因此有效的機械功率爲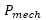
，所以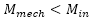
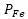爲電樞鐵(tiě)芯上(shàng)的損耗，也(yě)被成爲鐵(tiě)損，其中包括磁化過程中的磁滞損耗
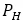，與頻率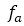
成正比，交變的電磁場在鐵(tiě)芯上(shàng)還有渦流損耗
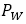，與頻率的平方
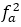成正比，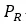
是轉子摩擦阻力的功率
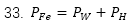
電機換向時(shí)電樞電流的突變頻率
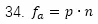
總效率爲總輸出功率除以總輸入功率，總電功率記爲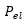
，除了(le)輸入電樞的功率
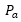，外(wài)部勵磁電流的功率也(yě)是輸入功率，因爲這(zhè)些(xiē)勵磁功率最後會(huì)轉變成熱損耗功率
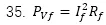
因此，總效率爲
